期待値とは

期待値とは、確率論における平均のことです。
期待値について以下の例で考えてみましょう。

ex) 以下のような学校の成績について考える。
・数学 I・A：評価 4
・数学 II・B：評価 4
・物理：評価 5
・化学：評価 3
・英語：評価 3

これらの成績の平均を考えると、以下のように計算・分解できます。

\begin{aligned}
\frac{2×4 + 1×5 + 2×3 }{2+5+2} = \frac{2×4 + 1×5 + 2×3 }{9} = 4×\frac{2}{9} + 5×\frac{1}{9} + 3×\frac{2}{9}
\end{aligned}

ここで、\(\frac{1}{9} = p(x_2), 5 = x_2\) のように抽象化して考えると、

\(x_1p(x_1)+x_2p(x_2)+x_3p(x_3)\)

のように書けます。これを一般化して、離散値の期待値は

\(\mathbb E [x] = \sum x p(x)\)

と表すことができます。

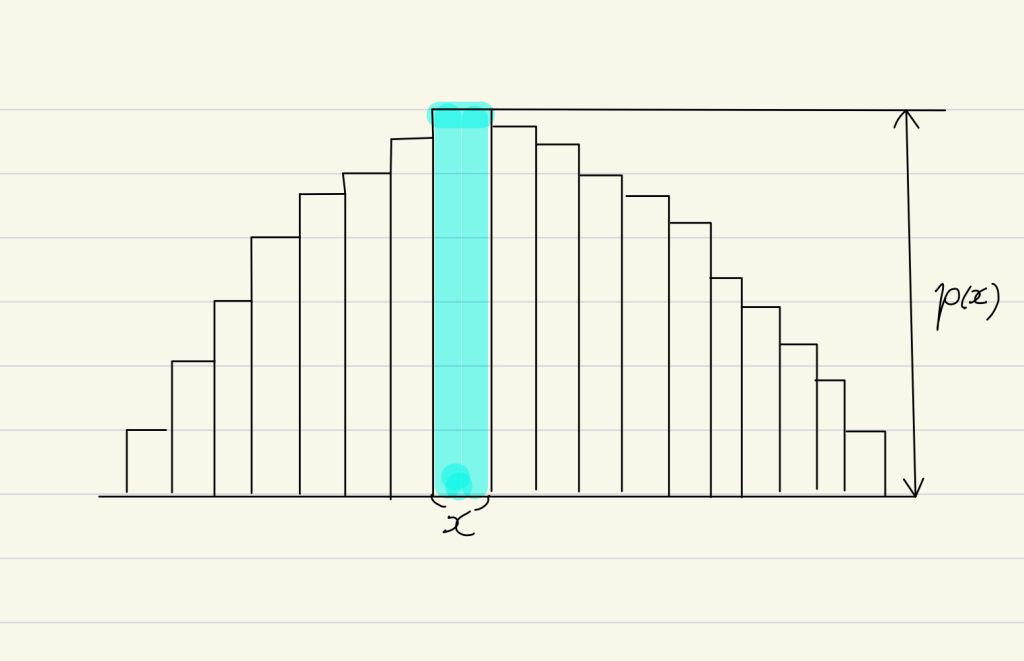
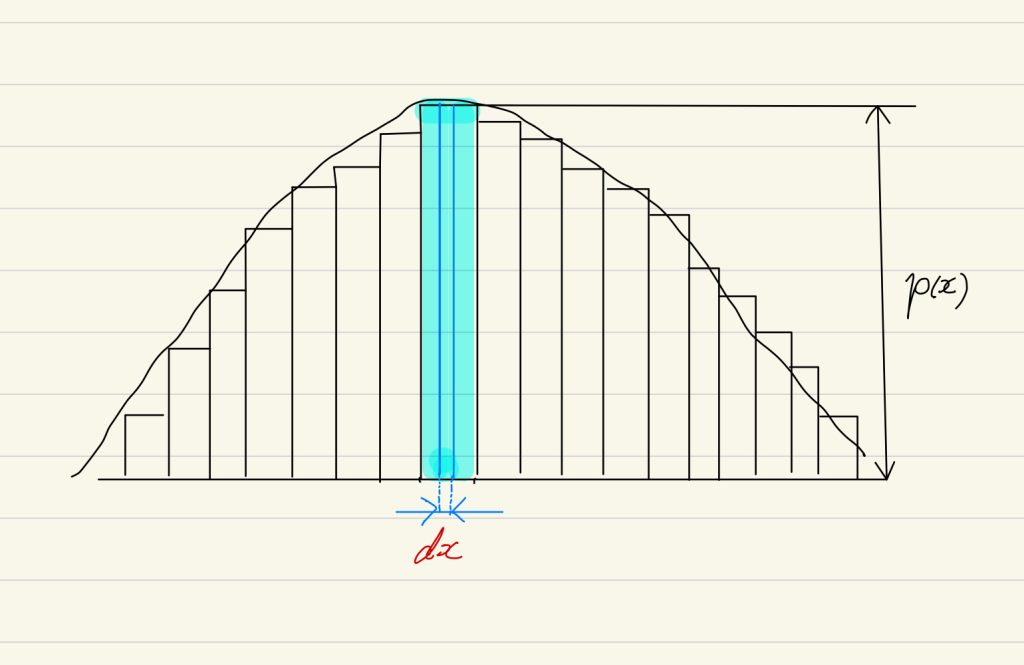
また、連続値の期待値については

\(\mathbb E[x] = \int xp(x)dx\)

と表すことができます。